The so called GUE hypothesis (see e.g. [1]) states that, in a certain limit, the
zeros of the Riemann zeta function on the critical line Re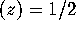 have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by
have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by 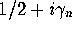 , where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit
, where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit 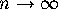 , with each
, with each 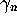 scaled by the
mean density of zeros at
scaled by the
mean density of zeros at 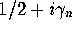
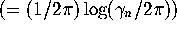 , so that the mean spacing between zeros is unity (any finite value will
do).
, so that the mean spacing between zeros is unity (any finite value will
do).
 Annotation Form Interface
Annotation Form Interface
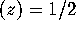 have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by
have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by 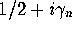 , where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit
, where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit 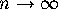 , with each
, with each 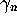 scaled by the
mean density of zeros at
scaled by the
mean density of zeros at 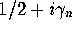
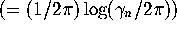 , so that the mean spacing between zeros is unity (any finite value will
do).
, so that the mean spacing between zeros is unity (any finite value will
do).