Consider the function f defined by 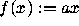 ,
where a>0. Given any initial point
,
where a>0. Given any initial point 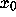 ,
it is clear that the dynamical system
,
it is clear that the dynamical system
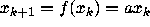 will have orbit
will have orbit

 Introduce a slight perturbation
Introduce a slight perturbation  to the initial
condition, say,
to the initial
condition, say, 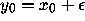 . The resulting orbit is:
. The resulting orbit is:

 So, after k iterations, these two orbits that started at
neighbouring points
So, after k iterations, these two orbits that started at
neighbouring points 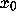 and
and 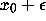 have separated
by
have separated
by 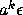 . Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.
. Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.
 Annotation Form Interface
Annotation Form Interface
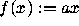 ,
where a>0. Given any initial point
,
where a>0. Given any initial point 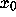 ,
it is clear that the dynamical system
,
it is clear that the dynamical system
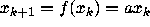 will have orbit
will have orbit

 Introduce a slight perturbation
Introduce a slight perturbation  to the initial
condition, say,
to the initial
condition, say, 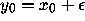 . The resulting orbit is:
. The resulting orbit is:

 So, after k iterations, these two orbits that started at
neighbouring points
So, after k iterations, these two orbits that started at
neighbouring points 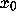 and
and 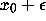 have separated
by
have separated
by 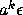 . Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.
. Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.