![[Shownotes]](../gif/annotate/sshow-151.gif)
 .
We simply choose some initial point more or less at random, say
.
We simply choose some initial point more or less at random, say 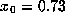 ,
and produce the first N iterates under the floating-point Gauss map, and
accumulate the average Lyapunov exponent.
At the end, this is supposed to be close to the exact almost-everywhere
Lyapunov exponent of the exact Gauss map,
,
and produce the first N iterates under the floating-point Gauss map, and
accumulate the average Lyapunov exponent.
At the end, this is supposed to be close to the exact almost-everywhere
Lyapunov exponent of the exact Gauss map, 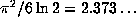 .
Well, if we know
.
Well, if we know 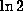 and can take square roots, this gives us the
value of
and can take square roots, this gives us the
value of  . Using the HP28S and 100,000 iterates of the floating-point
Gauss map with the above initial point, we get
. Using the HP28S and 100,000 iterates of the floating-point
Gauss map with the above initial point, we get 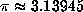 .
Note that this method relies on roundoff error, since without
it this orbit terminates!
.
Note that this method relies on roundoff error, since without
it this orbit terminates!